こんにちは、イブです。
エクセルを使用して有意差を求める方法について紹介します。
この手の情報を調べようとすると、謎の記号や数式が出現します。
日本語なのに「ちょっと何言ってるかわからない..」状態に陥ることもあります。
本記事では、あなたがなんとなく有意差のイメージを掴み、有意差を求めることができるようにします。

記事を読むとわかるようになること
●どういう場合に有意差を使用するのかわかる
●エクセルを使用して有意差を計算する方法がわかる
まず“有意差”自体がちょっと難しそうでヤダ..て人はこういうイメージを持っておけば大丈夫です。
要は”差があるかないか”です。
有意差について
以降は有意差とその求め方の説明をします。
抵抗がある人は説明部分を読み飛ばしてもOKです。
説明よりも早くやり方を教えてくれ!と思ったら下記リンクへ。
有意差とは
ある2つの事柄について、差があるかどうかを考えます。
差があることを有意差ありといいます。
(正確には2つ以上であればいいのですが、説明をシンプルにするため2つの比較の場合だけを考えます)
とはいえ、ものづくりにはばらつきがつきものですから、どれだけ頑張っても差は0にはなりません。
そこで、差の有無は実際にはこうなります。
基準となる値よりも差が大きい→差がある
基準となる値よりも差が小さい→差がない
“差がない=差が0” ではないのですね。
比較する2つのものに違いがないと仮定したときに、今考えている事象が起こる確率(p値)を考えます。
p値が一定以上⇒起こる確率が大きい→2つのものは違いがないと判断できる
(正確には“違いがないとはいえない”だが、“違いがない”と考えることが多い)
どんな時に使う?
さてこの有意差についてですが、製造業で差を評価するときに使います。
何かを変更するための評価で、もともと使用していたものと差があるか確かめる場面で大活躍です。
- 製品の改善のための変更
- 低コスト化のための変更
- 材料メーカー事情の変更
比較評価で知りたいこと
上記のような評価をする際、気になるポイントはこれです。
- 前と差があるのか、ないのか
- どの程度の差なら許容できるか
- 良くなったのか、悪くなったのか
製造業の評価で有意差を考える理由
有意差があるかわざわざ検証が必要なのは、先にも言いましたが、モノづくりにはばらつきがつきものだからです。
ばらつきが小さいほうがものづくりとしては良いですが、0にはなりません。
何も条件を変えずに生産しているのに、大きさが微妙に違ったり、強度が微妙に違ったりします。
何かを変更した評価の時に、その結果の差が製造のばらつきによるものなのか、それとも変更によるものなのか判定するために、この”有意差があるか”(もっと言うと、どこまでの差がついたら違う結果と判断するか)を考えることになります。

有意差検定の方法
有意差があるかないか判断するために、以下のような手法で検定を行います。
まず2つの質問に答える。
その結果によって使用するt検定の種類(全3種)が決まる。
後ほど、エクセルを使用して各検定を行う方法を紹介します。
説明よりもエクセルの検定のやり方を知りたい!という方はこちらへ。(記事後半に飛びます)
2群のデータに差があるか比較するときはt検定を使って調べることになりますが、2つのデータの関係性によって使用するt検定が3種類に分かれます。
※データのまとまり1つを1群といいます。
2つの質問の答えによって、3種類のどのt検定を使用するか決めます。
質問2:分散が等しいか 判断の仕方はこちら
Yes→分散が等しいときのt検定を実施(Bを参照)
No→分散が等しくないときのt検定を実施(Cを参照)
【関連用語紹介】検定の説明を理解するための基本用語
以下のような場合は2群間に対応があるとする
同じ対象に対して、複数の条件下で測定を行い、条件によって結果に差があるかを比較する(条件間の比較)
条件を同じにした複数の対象に対して測定を行い、対象によって結果に差があるかを比較する(対象間の比較)
分散はデータのばらつき具合を示す値です。
分散が大きい(平均値から離れた値をとるデータが多い)とばらつきが大きい、分散が少ないとばらつきが小さいことになります。
標準偏差は分散にルートをつけたもので、使用する意図は同じ(ばらつきや平均からの離れ具合を調べる)ですが、単位がデータの単位と同じになるためわかりやすく、一般的には標準偏差の方を使用することが多いかもしれません。
例 偏差値
受験の時によく聞く偏差値もこの標準偏差と関係があります。
偏差値は平均を50とし、そこからどれくらい離れた点数を取ったかを表したものです。
平均と関係のある値なので、同じ点数を取ったとしても学校単位で算出した偏差値と、全国の学生を対象に算出した偏差値が違うことになります。
有意差があるかないかを判断するための手法です。
方法は後ほど解説します。
分散が等しいかどうかを判断するための手法です。
方法は後ほど解説します。
3種類のt検定のうち、どれを使用するか
対応があるときのt検定(A)をする
分散が等しいか(等分散であるか)を調べる必要がなく、いきなりt検定を実施できます
対応あるt検定(分散分析)
対応するデータの差をとって新しく1群のデータを作り、その平均が0かどうかを検定します。
差が0→2群のデータ間に差はないと判定する
差が0でない→2群のデータ間に差があると判定する
従って検証対象の2つの群の分散(ばらつき)に差があるかどうかは気にしなくていいです。
分散が等しいかどうかをF検定によって調べます。
- データの個数が等しいとき⇒分散が等しいときのt検定(B)
- データの個数が等しくない⇒分散が等しくないときのt検定(C)
t検定のステップ(説明)
以下でt検定のステップについて説明しています。
これもちょっと頭痛くなりそう..って方は読み飛ばしOKです。
否定したい仮説(2群は差がない)を立て、それが間違っている(かなり起こりにくいことが起こっているので、誤っている。つまり2群は差がある)と判断するのがt検定です。
違いがないと仮定したときに、偶然に起こる確率を考えるというイメージです。
1.帰無仮説を立てる
仮説検定では知りたい事実と反対のことを仮説として設定します。
(否定したいこの仮説のことを、帰無仮説といいます)
(ちなみに、知りたい事実を帰無仮説と逆という意味で対立仮説といいます。)
2.優位水準を設定する
帰無仮説が成り立たない(対立仮説が成り立つ)と判断する基準を決めます。
優位水準に決まりはないですが、一般的には0.05(5%)を基準とすることが多いです。
3.t値を算出
t値(比較する2群に有意差があるか)を算出します
4.p値を算出
t値をもとにp値を算出します
5.p値と有意水準(❷で設定)を比較
p値<優位水準 なら、基準となる水準よりも珍しい(2つに差がないと仮定するとかなり起こりにくい)ことが起こっている
エクセルを使用したt検定の方法
ここからはエクセルを使用したt検定の方法を紹介していきます。
技術者必見です!
本ページを見ながらやってみてください。
関数で計算するやり方もありますが、アドインで分析ツールを入れておくと楽です。
エクセルを開き
ファイル→オプション

アドインで分析ツールを選択し、管理をExcel アドインにして設定を押します。

アドインのウィンドウが開くので、分析ツールにチェックを入れてOK
ここから、上記の2つの質問でわかった3つの検定を使い分けてやり方を紹介します。
A 対応があるときのt検定
B 分散が等しいときのt検定
C 分散が等しくないときのt検定
データ→データ分析

データ分析のウィンドウが開くので、“t検定:一対の標本による平均の検定”を選択し、OK
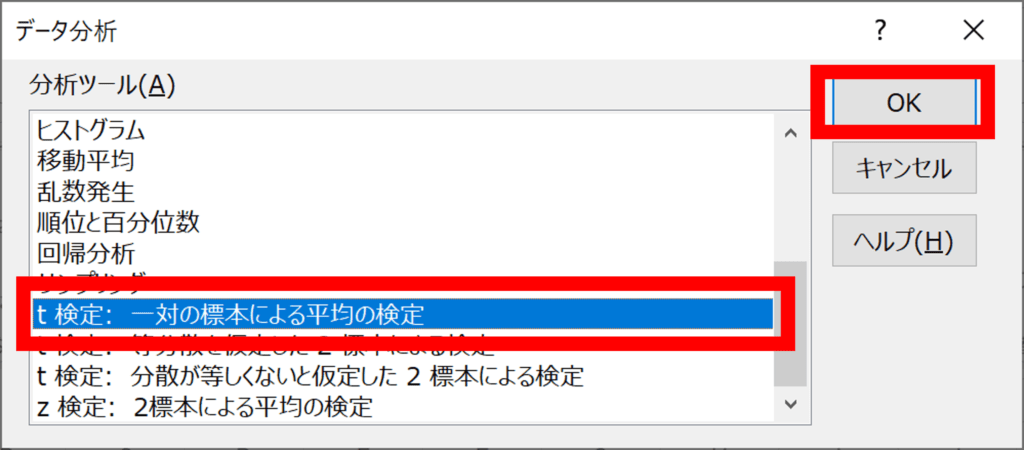
“t検定:一対の標本による平均の検定”のウィンドウが開くので、下記を入力してOK
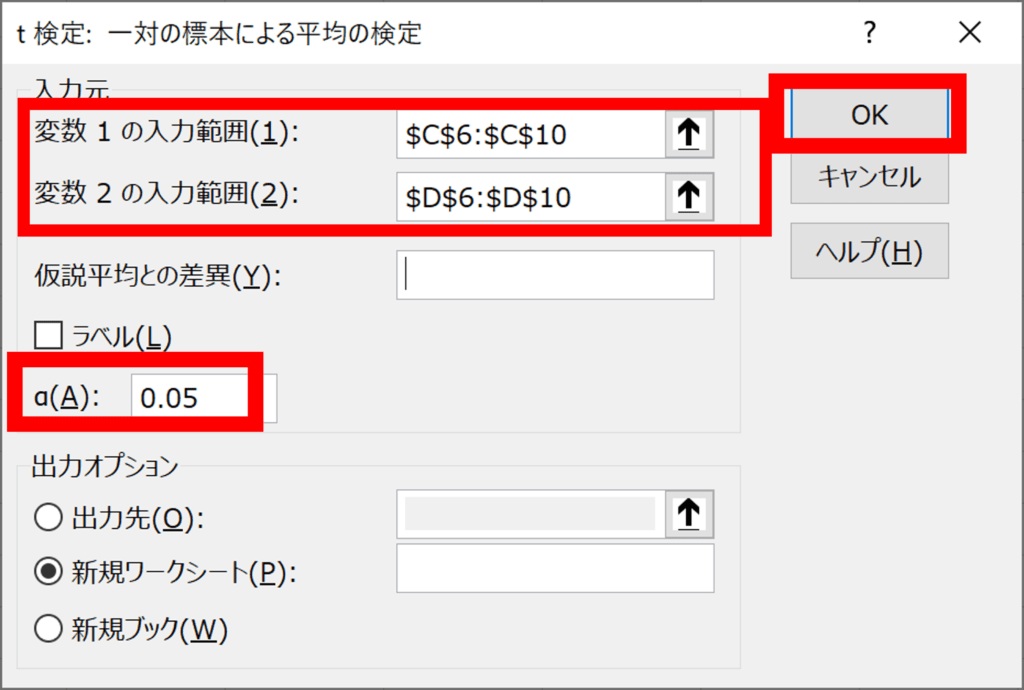
- 変数1、変数2に2群のデータをそれぞれ入力
- aに有意水準を入力(一般的には5%なので0.05を入力)
例
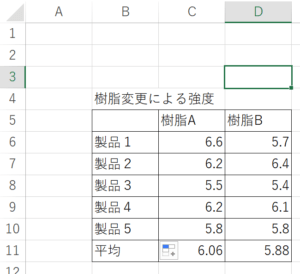
結果
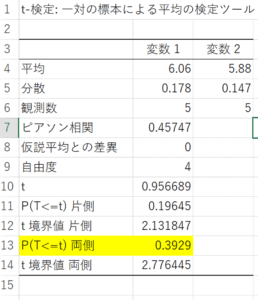
結果が表示されます。
P(p値)が0.05よりも大きいのか小さいのかを確認します。
P>0.05⇒有意差なし
P≦0.05⇒有意差あり
例では0.39<0.05なので有意差ありですね。
ここで、Pは(T<=t)両側、(T<=t)片側があると思いますが、分布が両側に伸びているか、片側かで判断すればOKです。
基本は両側になると思います。
データ→データ分析
データ分析のウィンドウが開くので、“t検定:等分散を仮定した2標本による検定”を選択し、OK
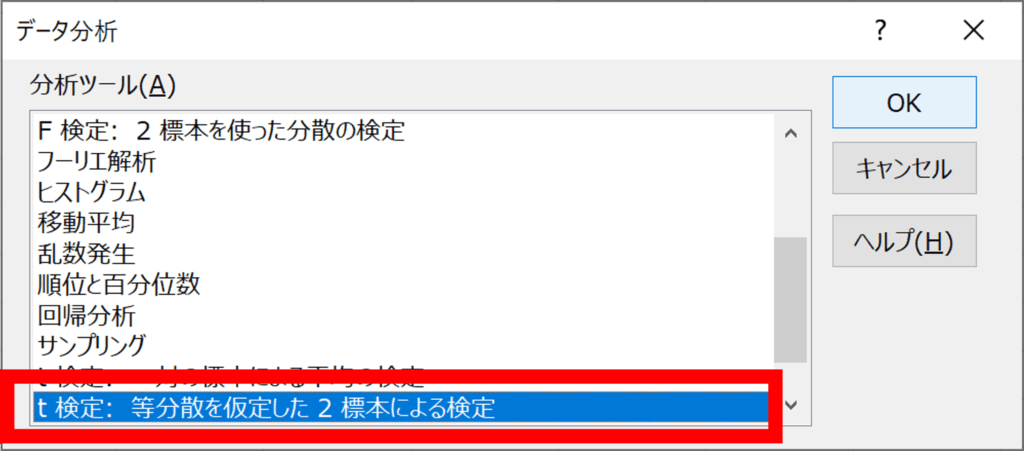
“t検定:等分散を仮定した2標本によるの検定”のウィンドウが開くので、下記を入力してOK
- 変数1、変数2に2群のデータをそれぞれ入力
- aに有意水準を入力(一般的には5%なので0.05を入力)
例
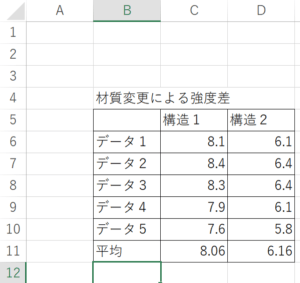
結果
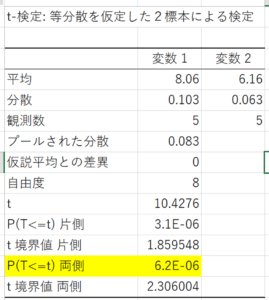
結果が表示されます。Aと同様に結果を判断します。
P(p値)が0.05よりも大きいのか小さいのかを確認します。
P>0.05⇒有意差なし
P≦0.05⇒有意差あり
例では0.000006<0.05なので有意差ありですね。
データ分析のウィンドウが開くので、“t検定:分散が等しくないと仮定した2標本による検定”を選択し、OK
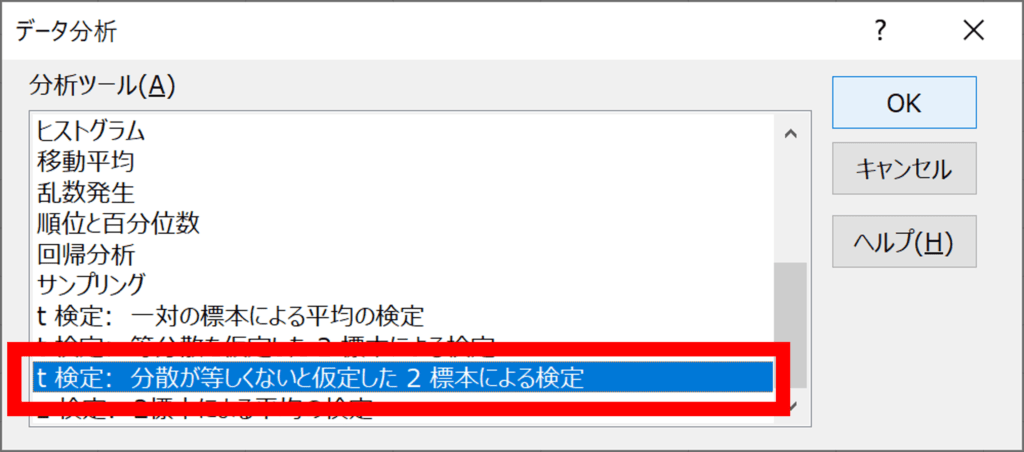
“t検定:分散が等しくないと仮定した2標本による検定”のウィンドウが開くので、下記を入力してOK
- 変数1、変数2に2群のデータをそれぞれ入力
- aに有意水準を入力(一般的には5%なので0.05を入力)
例
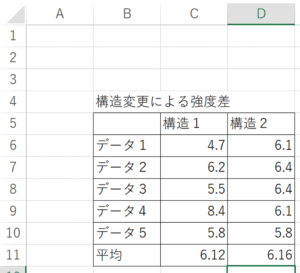
結果
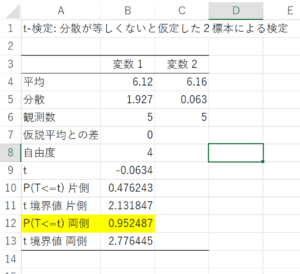
結果が表示されます。Aと同様に結果を判断します。
P(p値)が0.05よりも大きいのか小さいのかを確認します。
P>0.05⇒有意差なし
P≦0.05⇒有意差あり
例では0.93>0.05なので有意差なしですね。
(より正確には、有意差があるとは言えない、です。詳しくはコラム参照)
エクセルを使用したf検定の方法
t検定をする際、BかCか見分けるためにはF検定を行います。これもt検定を行うとき同様にエクセルを使用するとすぐにできます。
データ→データ分析
データ分析のウィンドウが開くので、“F検定:2標本を使った分散の検定”を選択し、OK
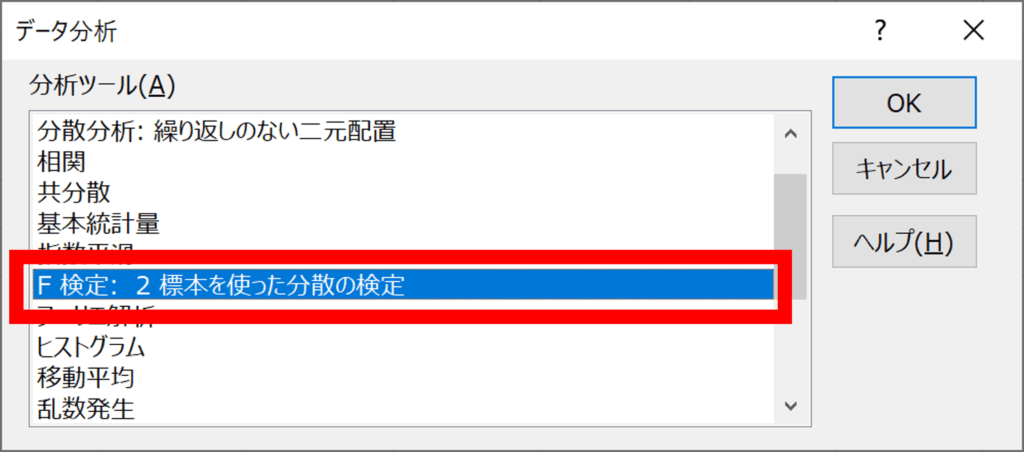
“F検定:2標本を使った分散の検定”のウィンドウが開くので、下記を入力してOK
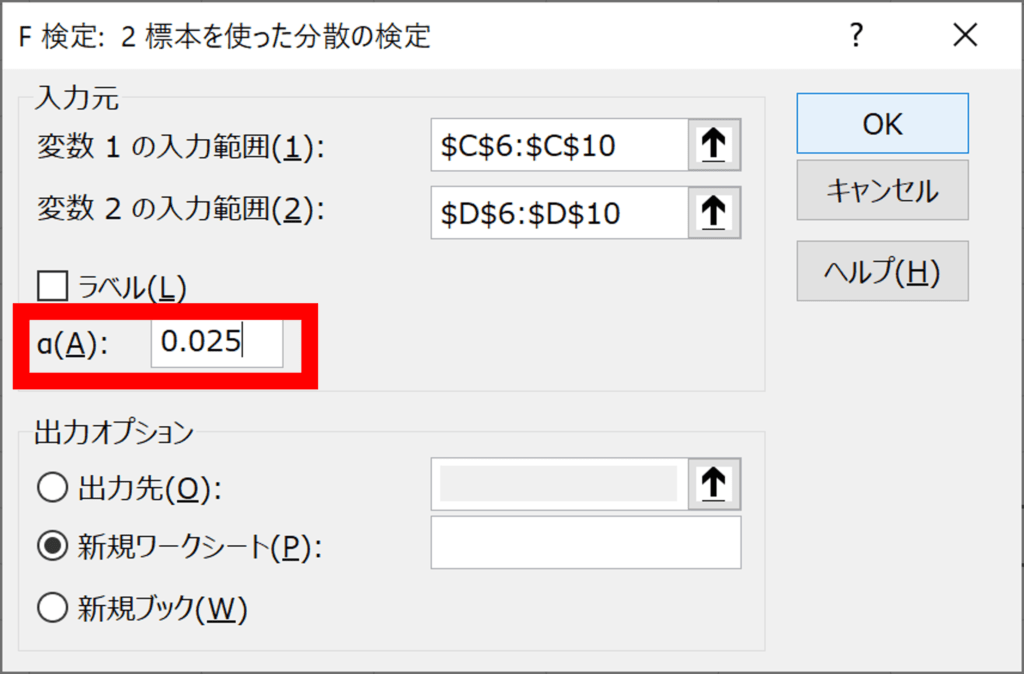
- 変数1、変数2に2群のデータをそれぞれ入力
- aに有意水準を入力(一般的には5%なので0.05。両側の場合は0.025を入力)
結果が表示されます。Aと同様に結果を判断します。
P(p値)が0.05よりも大きいのか小さいのかを確認します。
P>0.05⇒分散に有意差なし(分散が等しい)→t検定はBへ
P≦0.05⇒分散に有意差あり(分散が等しくない)→t検定はCへ
Bの例でf検定をした結果
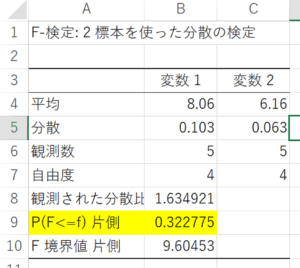
分散の有意差なし⇒分散が等しい
Cの例でf検定をした結果
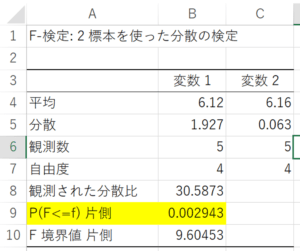
分散の有意差あり⇒分散が等しくない
コラム
”有意差がない=違いがない”という判断は間違だというNatureの論文が出ています。
「統計的有意差ではなく信頼区間を使うべき」との指摘もあります。
しかし、一般的には有意差があるか確認し、現行同等の実力があるか検証することも多いので、
そんな話もあるんだな、くらいに思っておけばいいと思います。
まとめ
有意差検定のやり方について紹介しました。
仕組みを理解するのは少々ややこしいですが、計算はエクセルを使用すれば簡単です。
●方法が決まれば、エクセルの機能により簡単に答えを出せる。
質問1:データ間に対応があるか
Yes→対応があるときのt検定を実施(Aを参照)
No→質問2へ
質問2:分散が等しいか
Yes→分散が等しいときのt検定を実施(Bを参照)
No→分散が等しくないときのt検定を実施(Cを参照)
仕事に役立つ知識でした。
エクセルの活用で仕事の幅が広がりますよ!!
●SEMを使いこなすコツについて
●仕事の悩み解決のヒント
●仕事、人間関係含む様々なストレスの対処法を紹介
以上、イブでした。
アダムとイブのTwitter(@bonjin_yusha)ではお役立ち情報を発信しています。







コメント
[…] […]